If you don't properly keep track of your coordinate system as you move from one position to the next along your spline, then your up vector may end up pointing in a random direction each time, causing your camera to rotate very unpredictably. Below is a summary of a method by Ken Sloan which you might use to move your up vector in a manner which doesn't nauseate the viewer!
Sloan's method decides each coordinate system using a function of the previous one, to ensure continuity. There are three vectors that we care about for each position P along the length of the spline--these are the tangent, the normal, and the binormal (often called T, N, and B, or collectively the Frenet Frame). The tangent is already known at each position--it can be acquired from the derivative of your spline function. The vectors which must be decided by this method are N and B.
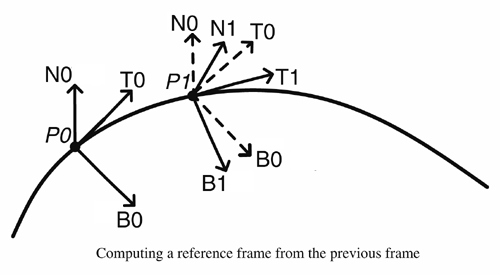
First, you'll need to generate your starting set of axes at point P0, given T0. The easiest way to do this (perhaps not the best) is as follows: Pick an arbitrary vector V. Make N0 = unit(T0 x V) and B0 = unit(T0 x N0), where unit(u) is the normalization of vector u, or u/|u|. You now have a starting set of coordinates.
Now you simply need a function to calculate a set of coordinate vectors given the previous set. Given a previous set at P0 and the desired new set at P1, a good way to do this is to let N1 = unit(B0 x T1) and B1 = unit(T1 x N1).

The coordinates as determined above are useful in two areas of the lab--the first is orienting the camera as it moves along the roller coaster. The second is deciding the orientation of features of the track itself (rails, cross-sections, etc) when you draw them to the screen. Both of these may be accomplished as a function of P, T, N, and B at any given point.