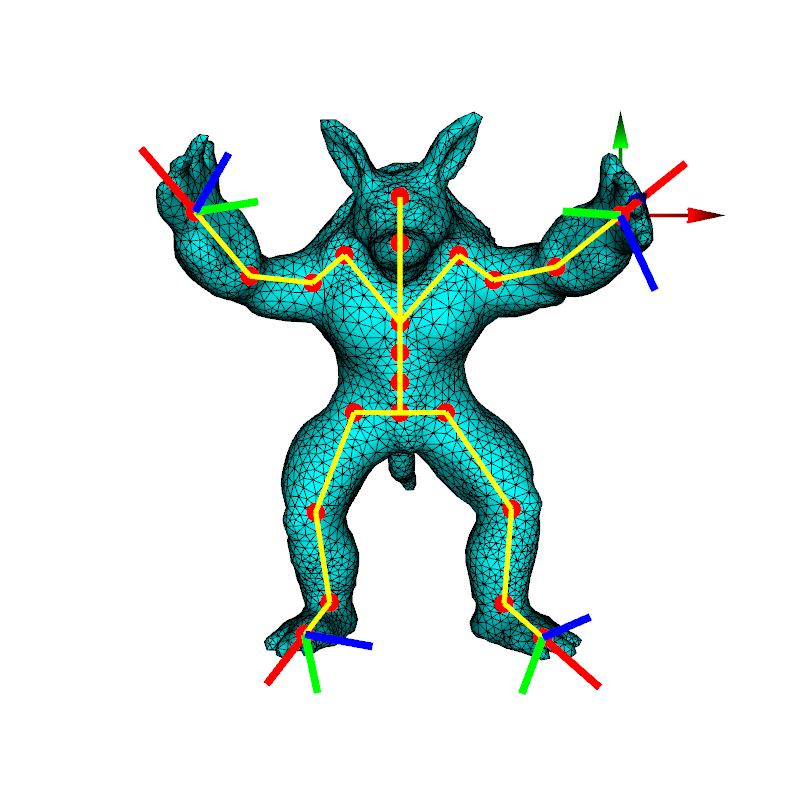
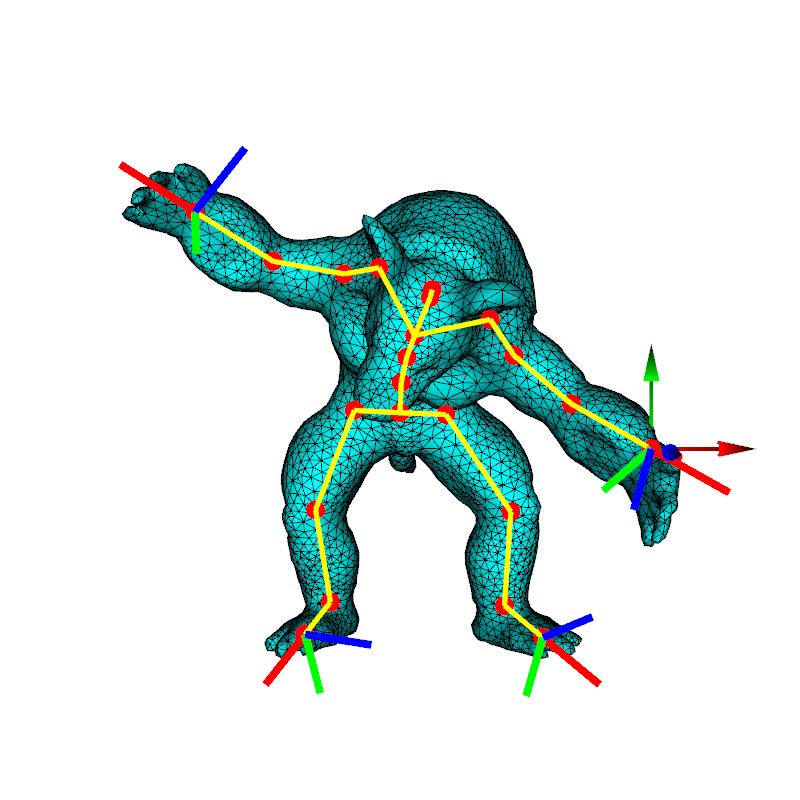
In this assignment, you will implement skinning, forward kinematics (FK) and inverse kinematics (IK) to deform a character. The character is represented as an obj mesh. We provide ASCII files for skinning weights and skeleton data. Our starter code can load the mesh, the skinning weights and the skeleton data, and render the mesh. Your task is to fill in the missing functions and code blocks to add skinning, FK and IK functionalities to the starter code.
You can download the starter code and data here.
First, we need to install some necessary tools for compiling ADOL-C. For MacOS (tested on 10.14.2), we recommend installing Homebrew. Homebrew is a MacOS software package management system that provides an easy way to use libraries on MacOS as if using them on Linux. Then, open Terminal, run $brew install autoconf automake libtool to install the tools. For Linux, run $sudo apt-get install autoconf automake libtool to install the tools. Next, enter the ADOL-C folder: <starter code folder>/adolc/sourceCode/, run command $autoreconf -fi to create a configure script. If no errors are reported, run $./configure to create a Makefile. If no errors are reported, run $make to compile the code. Finally run $make install to install ADOL-C at <your account's home folder>/adolc_base/. If you want to install ADOL-C at a different location, or if you want to customize, you can read <starter code folder>/adolc/sourceCode/INSTALL for more information. On Linux, you also need to add the path to ADOL-C libraries to LD_LIBRARY_PATH. For using ADOL-C, see https://core.ac.uk/download/pdf/62914383.pdf for a brief introduction. We also provide a simple example file ADOLCExample.cpp in the starter code which includes all the ADOL-C functions we need in this assignment.
In this assignment, OpenGL is used for rendering. For Windows and Linux users, no need to do anything for OpenGL. For Mac users, it is a little bit tricky: If you are using Mac OS X Mojave, make sure you update it to the latest version; otherwise, OpenGL errors can occur. Next, use Homebrew to install freeglut, which is an implementation of GLUT: $brew install freeglut (Note that although macOS comes with a GLUT framework, it is now deprecated and may not be stable.) Then, open Makefile, comment the line OPENGL_LIBS=-lGL -lGLU -lglut and uncomment OPENGL_LIBS=-framework OpenGL /usr/local/Cellar/freeglut/3.0.0/lib/libglut.dylib Now you should be able to compile the starter code in macOS.
Important: When you compile the starter code, you won't actually see the skeleton yet. Instead, you will see a picture that looks like the following. The skeleton should show up properly once you've implemented the function FK::computeLocalAndGlobalTransforms() in FK.cpp. The transformations that you compute in this function will automatically be used by the skeleton renderer to transform the joints to the proper positions.
The skeleton consists of several joints. Each joint has a parent joint, except the root joint. To implement skinning, each joint needs a skinning transform, which is a rigid transform: \(p \rightarrow R p + t\), where \(R\) is a \(3 \times 3\) rotation matrix and \(t\) is a \(3 \times 1\) vector. We can also use a \(4 \times 4\) matrix to represent the rigid transform, and use homogeneous coordinates to represent a 3D point. In this way, transforming a 3D point can be simplified to multiplying a \(4 \times 4\) transform matrix with the homogeneous coordinates of the point. We will use this representation for simplicity on this page. So for a mesh vertex \(i\) on the model, its position \(p_i\) is computed by skinning as: $$p_i = \sum_j w_j M_j^s \bar{p_i},$$ where \(\bar{p_i}\) is the homogeneous coordinates of the rest (a.k.a undeformed) position of the vertex, \(j\) goes over all the joints that affect the vertex, \(w_j\) is the skinning weight of joint \(j\) to the vertex and \(M_j^s\) is the joint's skinning transform matrix. You will need to implement this equation in skinning.cpp in the starter code.
Joints in the skeleton form a hierarchy. Each joint has a local transform. Using the hierarchy, we can compute the global transform of each joint. If joint "parent" is a parent of joint "child", then the global \(4 \times 4\) transform matrix of "child" is computed from the local transform matrix of "child" and the global transform matrix of the parent, $$M_{child}^g = M_{parent}^g M_{child}^l,$$ where \(M_i^g\) is the global transform matrix of joint \(i\) and \(M_i^l\) is the local transform matrix of joint \(i\). The local transform matrix is formed by its \(3 \times 3\) rotation matrix and \(3 \times 1\) translation vector. In this assignment, the local rotation matrix is computed using Euler angles, in the same way as in Autodesk Maya. All Euler angles in this assignment refer to the local rotation matrix between a parent and a child joint. Hence, we sometimes refer to them as the "local Euler angles", and sometimes simply as "Euler angles".
The starter code provides functionality to load the rest state Euler angles and rest local translation for each joint during initialization. It is written in FK.cpp. Here "rest" means the values assocated with the rest pose of the mesh. In this assignment, the local translations don't change at runtime, only the Euler angles. The input to the FK system are the Euler angles of each joint, and the output are the global transformations \(M_a^g\) of all the joints. You should first form local transformation matrices from the Euler angles, then traverse the joint hierarchy to form global transformation matrices from the local ones. You will need to implement this in FK.cpp.
Recall that skinning requires skinning transformation matrices for each joint. These are computed by FK too. For joint \(i\), the equation is $$M_i^s = M_i^g (\bar{M_i}^g)^{-1}, $$ where \(\bar{M_i}^g\) is the rest global transformation matrix. In the FK class constructor, you need to compute the rest global transformation matrices, and store them for re-use during runtime skinning.
The problem of IK is: Given target positions of several "end effectors", find the set of Euler angles at all the joints so that the "end effectors" assume their target positions (or get as close as possible to the target positions). The IK problem is usually under-constrained, and hence we need to also impose some regularization condition, such as, for example, minimize the magnitude of the joint angles or similar. In general, "end effectors" can be mesh vertices; but in this assignment, "end effectors" are a user-chosen subset of the joints. We call a joint that serves as an end effector a "handle". The position of a handle is the global translation of the joint. Let's define \(f(\theta)\) as the function whose input are all the Euler angles (in the entire joint hierarchy) and whose output are the handle joint global translations. Note that \(\theta\) is a vector of size \(n\), where \(n\) is \(3 \times \) the number of joints. The dimension of \(f\) is \(m\), where \(m\) is \(3 \times \) the number of IK handles. We must have \(m ≤ n\). We need the Jacobian matrix of \(f\) for solving IK. In this assignment, the Jacobian matrix is computed using ADOL-C. Use \(J\) to represent the Jacobian matrix of \(f\). The matrix \(J\) has \(m\) rows and \(n\) columns. We use Tikhonov regularization to perform IK. Formally, IK is computed by solving an optimization problem: $$\min_{\Delta \theta} {1 \over 2} \| J \Delta \theta - \Delta b\|^2 + {1 \over 2} \alpha \| \Delta \theta\|^2,$$ where \(\Delta b\) is a \(m \times 1\) vector representing the change of handle global positions, and \(\Delta \theta\) is a \(n\times 1\) vector representing the change of Euler angles we want to find. The term \({1 \over 2} \alpha \| \Delta \theta\|^2\) is a regularization term to avoid changing Euler angles too much; this tends to stabilize solution, at the cost of somewhat not meeting the required handle positions. Parameter \(\alpha\) determines how much regularization to add, and as such controls this tradeoff. Solving the optimization problem is equivalent to solving the following equation: $$(J^T J + \alpha I) \Delta \theta = J^T \Delta b,$$ where \(I\) is a \(n\times n\) identity matrix. You can use Eigen to compute the system matrix and the right-hand-side, and solve the linear system.
In the starter code, you will see several places marked with "Students should implement this." (or similar). These are the places where you need to provide your implementation. You do not need to modify driver.cpp (for core credit).
The assignment ships with three demos: armadillo, dragon, hand. You can switch between them by modifying run.sh.
You can change the manipulated IK handles by editing skin.config, field "*IKJointIDs". To obtain the ID of a joint, click on it with the mouse and look into the Terminal window.
Upload your entire solution as one zip file to the Blackboard. Don't forget to include your README file, the compiled executable (Windows or Mac, include all the required DLLs), the animation frames, and any other material required by the assignment writeup. For the animation, use the same format as with Assignment 1. Please submit JPEG frames (assumed frame rate is 15 fps), at the 800x600 resolution (or better). Do not exceed 600 frames.
Note: Blackboard has a limited upload bandwidth. To avoid uploading issues, please delete unnecessary files before submission. For example, Visual Studio will generate large redundant files. Remove them. Remove all object files (.obj, .o, or similar). Remove all intermediate compiling files (e.g. those in Debug/Release). Be careful to not accidentally erase your actual code files.
|
 |

|