Kirchhoff-Love Shells with Arbitrary Hyperelastic Materials
ACM SIGGRAPH Asia 2023
People
- Jiahao Wen
University of Southern California - Jernej Barbič
University of Southern California
Project material
Citation
-
Jiahao Wen, Jernej Barbič:
Kirchhoff-Love Shells with Arbitrary Hyperelastic Materials, ACM Transactions on Graphics 42(6) (SIGGRAPH Asia 2023), Dec 2023. BIBTEX
Abstract
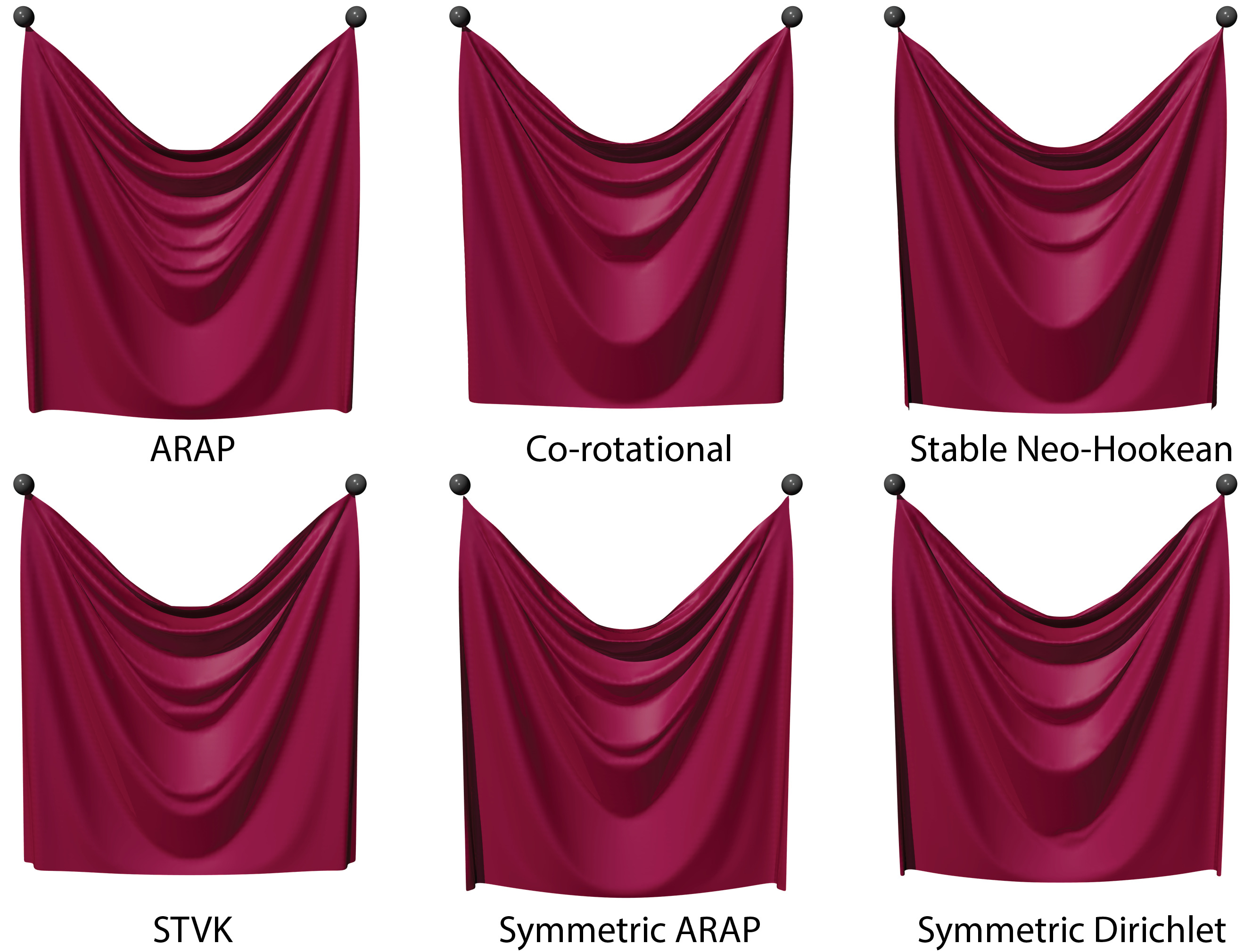
Kirchhoff-Love shells are commonly used in many branches of engineering, including in computer graphics, but have so far been simulated only under limited nonlinear material options. We derive the Kirchhoff-Love thin-shell mechanical energy for an arbitrary 3D volumetric hyperelastic material, including isotropic materials, anisotropic materials, and materials whereby the energy includes both even and odd powers of the principal stretches. We do this by starting with any 3D hyperelastic material, and then analytically computing the corresponding thin-shell energy limit. This explicitly identifies and separates in-plane stretching and bending terms, and avoids numerical quadrature. Thus, in-plane stretching and bending are shown to originate from one and the same process (volumetric elasticity of thin objects), as opposed to from two separate processes as done traditionally in cloth simulation. Because we can simulate materials that include both even and odd powers of stretches, we can accommodate standard mesh distortion energies previously employed for 3D solid simulations, such as Symmetric ARAP and Co-rotational materials. We relate the terms of our energy to those of prior work on Kirchhoff-Love thin-shells in computer graphics that assumed small in-plane stretches, and demonstrate the visual difference due to the presence of our exact stretching and bending terms. Furthermore, our formulation allows us to categorize all distinct hyperelastic Kirchhoff-Love thin-shell energies. Specifically, we prove that for Kirchhoff-Love thin-shells, the space of all hyperelastic materials collapses to two-dimensional hyperelastic materials. This observation enables us to create an interface for the design of thin-shell Kirchhoff-Love mechanical energies, which in turn enables us to create thin-shell materials that exhibit arbitrary stiffness profiles under large deformations.
Comments, questions to Jernej Barbič.
Errata
Errata for the paper.
Related projects
Acknowledgments
- NSF (IIS-1911224)
- USC Annerberg Graduate Fellowship to Jiahao Wen
- Bosch Research
- Adobe Research
Disclaimer
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Copyright notice
The documents contained in these directories are included by the contributing authors as a means to ensure timely dissemination of scholarly and technical work on a non-commercial basis. Copyright and all rights therein are maintained by the authors or by other copyright holders, notwithstanding that they have offered their works here electronically. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright. These works may not be reposted without the explicit permission of the copyright holder.
Unique accesses: